FP3級 2016年5月　実技（金財:個人）問3

【この問題にはが用意されています。読んでから回答してください。】

問3

Aさんが、60歳になるまでの10年間にわたって、年利1％で複利運用しながら毎年200万円を積み立てたうえで、この積立による10年後の元利合計金額を、60歳から5年間にわたって、年利1％で複利運用しながら毎年均等に取り崩して受け取る場合における毎年の受取金額は、次のうちどれか。なお、計算にあたっては下記の係数を用いることとし、〈答〉は万円未満を四捨五入して万円単位とする。また、税金や手数料等は考慮しないものとする。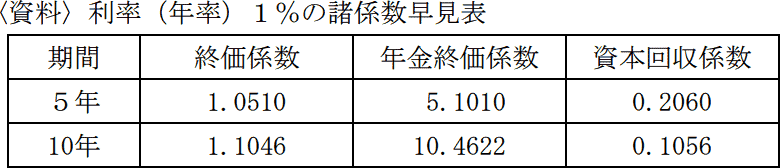
03.png/image-size:390×84
  1. 410万円
  2. 431万円
  3. 455万円
123
広告

正解　2

分野

科目：A.ライフプランニングと資金計画
細目：3.ライフプランニングの考え方・手法

解説

それぞれの係数は、預け入れたお金が一定利率で運用されると仮定した場合の、以下の金額を求める際に使います。
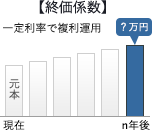
終価係数
現在のお金が将来いくらになるか
1/303.png/image-size:152×134
年金終価係数
毎年同じ金額を積立て続けると、将来合計でいくらになるか
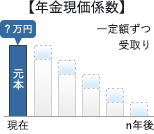
1/307.png/image-size:154×134
資本回収係数
現在あるお金を毎年均等に受け取ると、毎年いくらになるか
1/308.png/image-size:150×134
本問では、まず10年間一定金額を積み立てた場合の合計額を年金終価係数を使用して求め、次に、その合計額を5年間で毎年均等に取り崩して受け取る場合における毎年の受取金額を資本回収係数を使用して求めるという2段階の計算が必要になります。

Aさんは10年間にわたり年利1％で複利運用しながら毎年200万円を積み立てるので、60歳時点の元利合計額は、

　200万円×10.4622＝2092.44万円

その後、年利1％で複利運用しながら5年間均等に取り崩すので、毎年の受取金額は、

　2092.44万円×0.2060＝431.04…万円
（万円未満四捨五入）431万円

したがって[2]が正解です。
広告