FP3級 2017年9月　実技（FP協会:資産設計）問17

【この問題にはが用意されています。読んでから回答してください。】

問17

宏光さんは、今後15年間で毎年20万円ずつ積立貯蓄をして、長男の風磨さんの教育資金を準備したいと考えている。積立期間中に年利2％で複利運用できるものとした場合、15年後の合計額として、正しいものはどれか。なお、下記＜資料＞の3つの係数の中から最も適切な係数を選択して計算し、解答に当たっては、千円未満を四捨五入すること。また、税金や記載のない事項については一切考慮しないこととする。
17.png/image-size:353×68
  1. 4,038,000円
  2. 3,459,000円
  3. 2,570,000円
123
広告

正解　2

分野

科目：A.ライフプランニングと資金計画
細目：3.ライフプランニングの考え方・手法

解説

「毎年一定金額を積み立て」とくれば、使うのは「年金終価係数」または「減債基金係数」のどちらかです。設問のケースでは一定期間後の元利合計額を求めたいので「年金終価係数」を用いるのが適切です。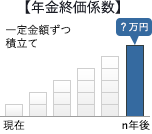
1/305.png/image-size:152×134
係数は原則として乗算で使用するので、毎年の積立額20万円に年金終価係数17.293を乗じて15年後の積立金額を求めます。

　200,000円×17.293＝3,458,600円
（千円未満を四捨五入）3,459,000円

したがって[2]が正解です。
広告