FP3級過去問題 2015年5月学科試験 問31

問31

利率（年率）2％で複利運用しながら毎年一定額を積み立て、15年後に6,000,000円を準備する場合、毎年の積立金額は、下記〈資料〉の係数を使用して算出すると（）となる。
31.png/image-size:310×61
  1. 297,200円
  2. 346,800円
  3. 466,800円
123
広告

正解　2

問題難易度
肢14.0%
肢285.3%
肢310.7%

分野

科目：A.ライフプランニングと資金計画
細目：3.ライフプランニングの考え方・手法

解説

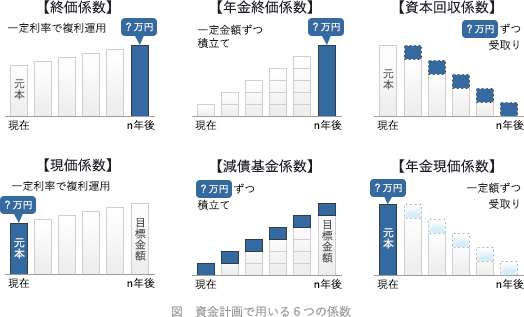
資金計画を立てる際に用いる係数には以下の6つがあります。
終価係数
現在の金額を一定利率で複利運用した場合のn年後の元利合計額を求める
現価係数
一定利率で複利運用するとして、n年後に一定金額に達するために必要な元本を求める
年金終価係数
毎年一定金額を積み立てた場合のn年後の元利合計額を求める
減債基金係数
n年後に一定金額に達するために必要な毎年の積立額を求める
資本回収係数
現在の金額をn年間で取り崩した場合の毎年の受取額を求める
年金現価係数
n年間にわたり一定金額を受け取るために必要な元本を求める
1/300.png/image-size:524×317
「毎年一定金額を積み立て」とくれば、使うのは「年金終価係数」または「減債基金係数」のいずれかです。設問のケースでは目標金額に達するために必要な「毎年の積立金額」を知りたいので「減債基金係数」を用います。

　6,000,000円×0.0578＝346,800円

したがって[2]が適切です。
広告